Re: [討論] L1L2正規化的物理意義。

看板DataScience作者f496328mm (123)時間5年前 (2019/01/10 13:54)推噓5(5推 0噓 15→)

留言20則, 5人參與討論串2/3 (看更多)

※ 引述《peter308 (pete)》之銘言： : L1L2是一種常見的正規化技巧 : 用來降低過度擬和效應的程度 : 我最近發現其背後有非常深刻的物理意義 : 首先我們通常都會定義一個loss function 並加上L1 L2項 : https://i.imgur.com/5OUdn1e.png

: 如果學過古典力學的同學應該都知道有個Euler-Lagrange eq : 而 λ1、λ2 分別對應Euler-Lagrange eq中的兩個不同Lagrangian Multipliers : 後面的加總項則稱為L^1 、L^2 norm : L^1 L^2 norm可以看成是兩個個別的邊界條件 : 所以前面那項loss function 可以看成是 δS 或是最小作用量 (least Action ) : S就是Action 通常會是Lagrangian L 的一個路徑積分 S:=∫Ldt t:= time : 因為很多我們感興趣的系統都是很複雜的 : 所以我們根本無從得知其Action或是Lagrangian的實際數學表示式， : 也就無法對其做變分來了解其動力學了。 : 所以只能用類神經網路模型或是其他的機器學習模型在數值上做逼近 : 但我覺得整個(minimize loss Function+L1L2)精神 : 和Euler-Lagrange variation Eq 是等價的 : L1 L2-norm 其實也可以推廣到 L^p norm (P=0~Inf) : L^p norm 的 L其實就是 Lebesgue (一個數學家的人名) : 某個L^P 就定義出一個metric space (可以用來量測數據點之間的距離) : L^2 就是歐式空間距離 : L^1 則叫做 Manhattan norm : 所以各位可以把L1L2正規化看成是 : 引入兩個L^1 metric space和 L^2 metric space邊條件 : 加在原本loss function上的一種變分的數值方法 : 不過話說回來 : 怎麼知道數據點一定是在 L^1 space或是 L^2 space上呢? : 它不能再其他的 L^p space上嗎?? : 簡單說 : 為啥邊條件只假設設定在 L^1 space 或是 L^2 space上? 這要回到最基礎的回歸問題我們希望找出 y = x1*beta1 + x2*beta2 ... 背後的多項式解法就是最小化 y - sum( x_i*beta_i ) x 越多會 fit 的越準( train 的情況下 )，為了避免這種極端狀況要懲罰選太多變數(x) 的情況，所以變成這樣 y - sum( x_i*beta_i ) + λ*sum( beta_i ) 這樣如果選太多 x ( 也就是 x 前的係數 beta_i 太多不為 0 ) 會不容易讓上面的式子最小化這樣的好處是，我們可以知道，選哪些變數，會最小化上面的式子，也就是 variable selection L1 norm, L2 norm 只是一開始的基礎想法，另外這樣也不會使計算太複雜( 以前人沒有電腦 ) 而 L1 norm 最大的好處，可以參考下面這張圖 https://pic4.zhimg.com/v2-81b39b76d0d43229f32b216c99287a3d_1200x500.jpg

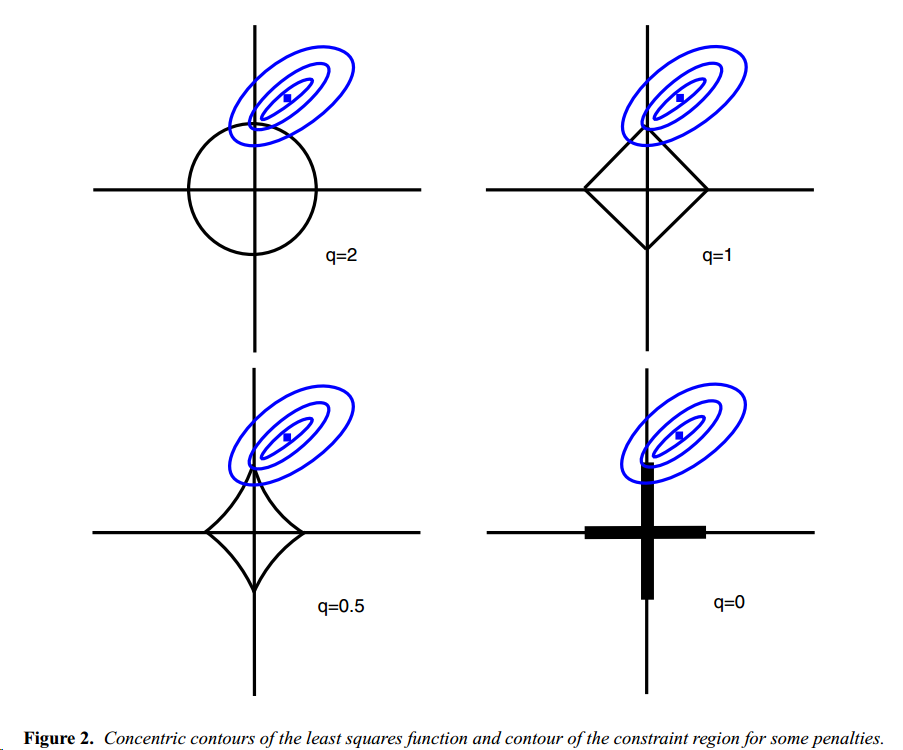
q 代表次方數, x軸y軸代表你的變數 ( x1,x2... ) 的 beta 橢圓形是( y-x*beta )我們要逼近的式子( 這有點忘了QQ ) 當橢圓與菱形交會點，就是最小化的點，也就是我們所求的多項式的 beta_i L1 norm 可以更容易接觸到端點 ( 尖尖的部分 ) 這好處是，可以讓其中一個變數(x) beta 為0，不去選它，這就是 variable selection 的重點，使用越少變數，去解釋 model 這就是為什麼使用 L1 norm 你當然也可以用 L3,L4 等等，但其實到後面，意義就不大了我們通常都希望，找出重要變數，用越少 X 去解釋 model，所以 L1 比較常用 L1 norm 還有個特別的名稱， lasso lasso 後面還有更多延伸，例如針對不同 beta 使用不同 lambda，逞罰程度不同這方面有興趣可以再 google -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 60.248.26.145 ※ 文章網址: https://www.ptt.cc/bbs/DataScience/M.1547099645.A.AE5.html

推

peter308

01/11 15:26, 5年前 , 1^F

01/11 15:26, 1^F

→

peter308

01/11 15:27, 5年前 , 2^F

01/11 15:27, 2^F

→

f496328mm

01/11 20:21, 5年前 , 3^F

01/11 20:21, 3^F